音楽理論講座ー音程
freeze
contents
音程について
音程というと皆さんはどんなことを想像するでしょうか。例えばポケモンのプリンは12オクターブまでの音程で歌えるとかいったようなそんなことでしょうか。音程とは音と音との高さの隔たりを表す言葉です。例えばC(ド)の半音高いC#(ド#)とCとの音程はどのぐらいですかと聞かれたらその半音分ですと言えばいいわけです。
しかし、いっつもいっつも半音分だとか、1/2オクターブ分だねとかと言うのは面倒くさいので、音楽の世界では度数という単位で表します。
度数とは基になる音からある音がどのくらい高さがあるかを示すもので、「~度」という風にカウントします。
例えば、C(ド)からD(レ)までは何度ですかと聞かれたら、まずCが基となる音ですから1度、さらにDはお隣さんなので1,2という感じで、CとDの間は2度とカウントすることができます。
ref
上は度数の一覧表です参考にしてください
上の表を見ると同じ音同士だったら1度、一つ違えば2度、2つ違えば3度だとわかりますね
12平均律
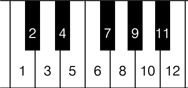
12平均律とは1オクターヴ(C~次のCまで)を音程を等しい比で12等分したもので、細かいことは省きますが、とにかく音が綺麗に変化していく様を表した様式で、よく見る例だとピアノの鍵盤にもちいられています。(以下画像)
br
ref
br
こんな風に1オクターヴを12等分しています。
度数の種類
さて、大体音程のことについてよくわかってきましたが、ここで一つ問題をやってみましょう。
「CとC#の度数をこたえよ」
br
こう聞かれた時、どう答えますか?
同じCとCなら1度とあらわせるけど,#がついているからどうにも1度とは表せないし、かと言って2度と答えるのも何か違うような気がするのではないでしょうか。こういう場合は前述の原則に従ってみましょう
CとC#は元々同じCの音ですからその差は一度です。ただ、一度は一度なのですが、CとC#の間には半音の差があるので、一度とだけ表すことはできません。
この半音の差を示すために、音楽理論では度数の性質に合わせた数え方をします。
 SEAP22マニュアル
SEAP22マニュアル